支援向量機（Support Vector Machine，SVM）

• 用於監督式學習中的分類和回歸
• 找到一個超平面將不同類別的數據點分開，同時最大化兩個類別之間的邊界
• 常用於二分類（binary classification）

超參數

• 例如正則化參數C、內核類型、內核參數等
• 影響模型的性能和泛化能力

SVM Kernel

線性核函數（Linear Kernel）：kernel='linear'

• 使用線性函數計算內積，適用於線性可分的問題。

• 投影方法

多項式核函數（Polynomial Kernel）：kernel='poly'

• 使用多項式函數計算內積，適用於非線性可分的問題。

径向基函數（Radial Basis Function, RBF Kernel）：kernel='rbf'

• 使用高斯函數計算內積，適用於非線性可分的問題。

三角核函數（Triangular Kernel）：kernel='triangular'

• 使用三角函數計算內積。

高斯核函數（Gaussian Kernel）：kernel='gaussian'

• 使用高斯函數計算內積。

指數核函數（Exponential Kernel）：kernel='exponential'

• 使用指數函數計算內積。

Sigmoid 核函數（Sigmoid Kernel）：kernel='sigmoid'

• 使用 sigmoid 函數計算內積。

超平面（Hyperplane）：

在幾何學和線性代數中，超平面是一個維度比其所在的空間低一的平面。在支援向量機的上下文中，我們通常談論的是二維或三維空間中的超平面，但它們的定義可以擴展到更高維度的空間。

二維空間中的超平面：

在二維平面中，超平面是一條直線，可以將平面分成兩個區域。這條直線滿足以下特性：

它是平面上的一個線性方程的解，通常表示為Ax + By + C = 0，其中A、B和C是常數，且A和B不同於零。
當Ax + By + C的值為正時，點位於直線的一側，而當值為負時，點位於直線的另一側。

三維空間中的超平面：

• 最大化兩個類別之間的邊界（支持向量之間的距離）。
• 將不同類別的數據點正確分類到超平面的不同側。

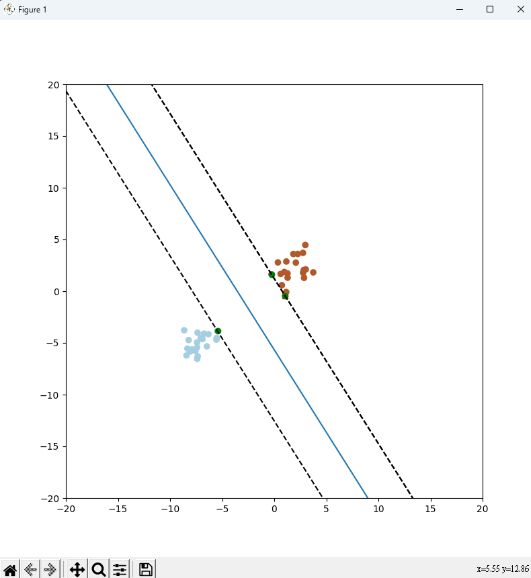
在三維空間中，超平面是一個平面，可以將三維空間分成兩個區域。這個平面滿足類似的特性：

它是三維空間中的一個線性方程的解，通常表示為Ax + By + Cz + D = 0，其中A、B、C和D是常數，且A、B和C不同於零。
當Ax + By + Cz + D的值為正時，點位於平面的一側，而當值為負時，點位於平面的另一側。
超平面在SVM中的應用：
在SVM中，超平面扮演著關鍵的角色，因為它用於區分不同類別的數據點。SVM的目標是找到一個最佳的超平面

推薦這篇文: https://chunyeung.medium.com/%E6%B7%B1%E5%BA%A6%E5%AD%B8%E7%BF%92-%E8%B6%85%E5%B9%B3%E9%9D%A2-hyperplane-bf05940bb3fd

SVM範例

# 引入必要的庫
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn import svm
from sklearn.model_selection import train_test_split

# 生成示例數據集
X, y = datasets.make_classification(
    n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)

# 將數據集分為訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42)

# 初始化SVM分類器
svm_classifier = svm.SVC(kernel='linear')  # 我們使用線性內核

# 訓練SVM模型
svm_classifier.fit(X_train, y_train)

# 進行預測
y_pred = svm_classifier.predict(X_test)

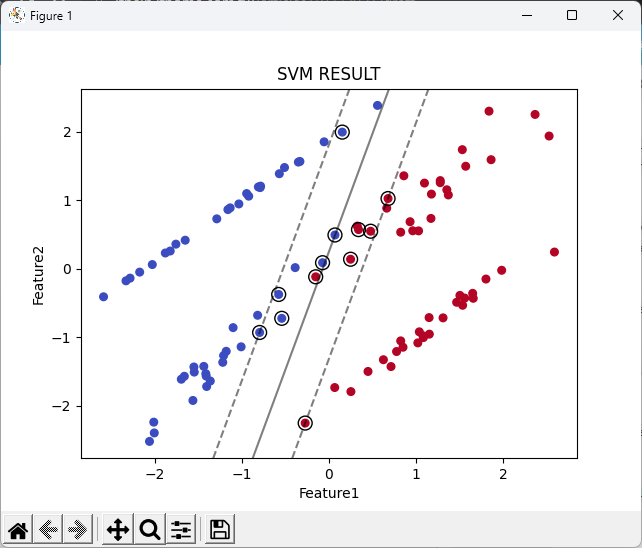
# 繪製數據點
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='coolwarm', s=30)

# 繪製決策邊界
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 50),
                     np.linspace(ylim[0], ylim[1], 50))
Z = svm_classifier.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contour(xx, yy, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
            linestyles=['--', '-', '--'])

# 繪製支持向量
plt.scatter(svm_classifier.support_vectors_[:, 0], svm_classifier.support_vectors_[:, 1],
            s=100, facecolors='none', edgecolors='k')

plt.title('SVM RESULT')
plt.xlabel('Feature1')
plt.ylabel('Feature2')
plt.show()

應用

• 文本分類: 自然語言處理（NLP）
• 影像識別: 圖像識別、人臉識別、物體檢測
• 金融領域: 信用評估、股票市場預測、詐騙檢測
• 推薦系統: 個性化推薦系統
• 手寫識別: 光學字符識別（OCR）
• 品質管理: 工業自動化和品質控制